算法图解
第一章 算法简介
1.1认识
算法是一组完成任务的指令。任何代码片段都可以视为算法。
1.2二分查找
二分查找是一种算法,其输入是一个有序的元素列表,如果要查找的元素包含在列表中,二分查找返回其位置;否则返回null
二分查找就是在有序的列表中,每一次查看中间的值满不满足条件,一下就能排除一半的数据。就像是在100里面查找数据,从50开始猜,每一次告诉你猜大了还是猜小了,从50开始猜就会一下排除50个数据,以此类推。
在后续我们提到log的时候,我们就把把他当做是log2。
如果使用二分法查找八个数据中的其中一个,那么最多查找log8次,也就是三次。
下面是一个二分查找的python例子
函数binary_search接受一个有序数组和一个元素。如果指定的元素包含在数组中,这个函数将返回其位置。
lisst = [1,2,3,4,5,6]
def binary_search(listx,item):
low = 0
high = len(listx)-1
while low <=high:
mid = int((low + high) / 2)
guess = listx[mid]
if item<guess:
high = mid-1
elif item > guess:
low = mid+1
elif item == guess:
return mid
else:
return None
print(binary_search(lisst,4))
1.2.1运算时间
每次介绍算法时,我们都将讨论他们的运算时间。
最多需要猜测的次数与列表长度相同,这杯称为线性时间。
1.3大O表示法
大O表示法是一种特殊的表示法,指出了算法的速度有多快。
O(n):中间的n就是操作数,操作数越大,所用的时间就越长。例如用二分法查找十六个数据,则是O(log 16);而用简单查找法则是O(16).
大O表示法指出了最糟糕情况下的运行时间,即运行时间永远不可能超过大O表示法所表示的时间。
1.3.1一些常见的大O运行时间
下面从快到慢列出
O(log n)也叫对数时间,这样的算法包括二分查找
O(n) 也叫线性时间,这样的算法包括简单查找。
O(n*log n)。这样的算法包括第四章简要介绍的快速排序,一种速度较快的排序算法。
O(n**2),这样的算法包括第二章简要介绍的选择排序, 一种速度较慢的排序算法。
O(n!),这样的算法包括接下来将介绍的旅行商问题的解决方法,一种非常慢的算法。
启示:
1.算法的速度指的并非时间,而是操作数的增速。
2.谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
3.算法的运行时间用大O表示法表示。
1.3.2旅行商
O(n!)的算法解决了计算机科学领域非常著名的旅行商问题。
一位旅行商要前往五个城市,同时要确保旅程最短,对于每种城市排序,他都计算总旅程,在涉及五个城市时,他需要计算120次操作。
6个城市时,他需要计算720次,计算的次数按照几何倍的增长,这种算法很糟糕,但是目前还没有找到更快的算法,我们别无他发。
第二章 选择排序
2.1内存
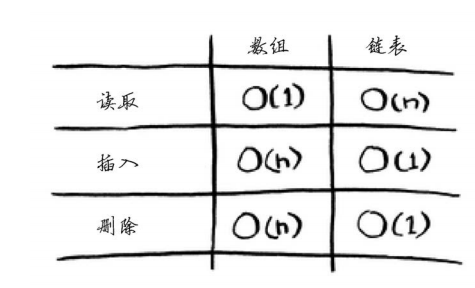
2.1.1链表
相较于数组,链表可以储存在内存的任何一个空间,每一个空间中都存储有下一个空间的地址,这样就实现了将随机内存地址串联起来。
2.1.2数组
虽然数组的内存地址必须相邻,但是同样也有链表不具备的好处,链表要查找信息的时候,并不能直接查找最后一和数据的内容,因为我们还不知道他的内存地址,我们需要一个一个数据的查看才能获取最后一个数据的地址。但是数组因为数据是相邻的,所以我们可以直接查看任意位置的数据内容。
2.1.3数据插入和删除
链表的数据插入很简单,只需要让前一个地址指向插入的地址,再由插入的地址指向洗衣歌地址。
宿主的插入则需要让每一个后面的元素的索引加一。
删除是同样的道理,数组的索引会改变。
下面是常见数组和链表操作的运行时间。
2.2选择排序
给一串无序列表排序,先创建一个新的列表,然后在旧列表中找到最大的那个放入新列表中,然后再找到第二大的放入新列表中,以此类推,最后排序成功。这就是选择排序,是一种效率极其低下的排序算法。
第三章 递归
3.1递归和循环
如果使用循环,程序的性能可能更高;如果使用递归,程序更容易理解
3.2基线条件和递归条件
每一个递归函数都有两个部分,基线条件和递归条件。递归条件是指函数调用自己的条件,基线条件则是函数不在调用自己的条件,从而避免形成无限循环。
3.3栈
栈是一种数据结构,我们只能对他使用两种操作模式,在最后面添加,或者删除最后面的元素。
3.3.1调用栈(call stack)
计算机在内部使用被称为调用栈的栈。调用栈最经常被用于存放子程序的返回地址。在调用任何子程序时,主程序都必须暂存子程序运行完毕后应该返回到的地址。
3.3.2递归调用栈
每重新调用函数就会增加一层调用栈,直到基线条件满足则不断弹出每一层的调用栈。
第四章 快速排序
4.1分而治之
divide and conquer D&C
一种著名的递归式问题解决方法。
根据dc的定义,每一次递归都必须缩小问题规模。
D&C的工作原理:
(1)找出简单的基线条件;
(2)确定如何缩小问题的规模,使其符合基线条件。
例子:用dc来计算一个列表中的和。
result = 0
def new_sum(listx):
global result
if len(listx) > 0:
a = listx[0]
listx.pop(0)
result += a
new_sum(listx)
else:
print(result)
asd = [1,2,3]
new_sum(asd)
4.2 快速排序
快速排序是一种常用的排序算法,比选择排序快很多。例如c语言标准库中的函数qsort实现的就是款速排序。快速排序也使用了D&C。
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
下面是快速排序算法的python代码:
def quksort(listx):
if len(listx)<2:
return listx
else:
minder = listx[0]
small = []
big = []
for i,item in enumerate(listx):
if i == 0:
pass
elif item >= minder:
small.append(item)
else:
big.append(item)
return quksort(small)+[minder]+quksort(big)
data = [1,5,6,3,3,2,4]
print(quksort(data))
第五章 散列表
就是python中的字典
第六章 广度优先搜索
广度优先搜索(也称宽度优先搜索,缩写BFS,以下采用广度来描述)是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,故得名。
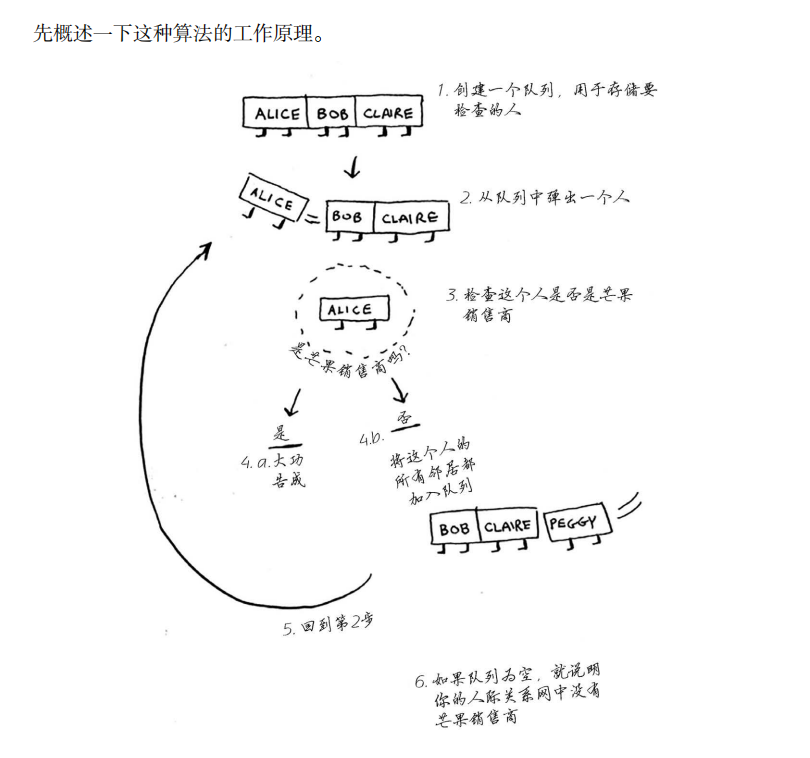
第七章 狄克斯特拉算法
7.1术语
7.2作用
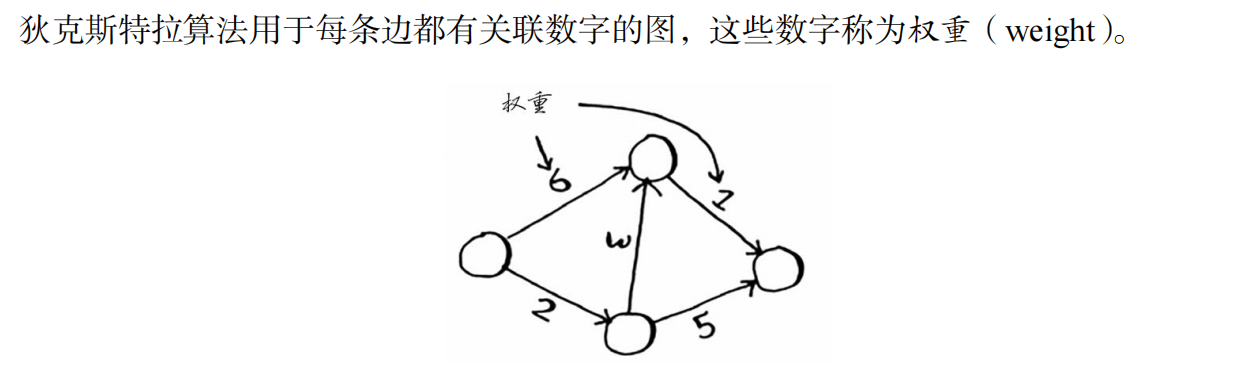
在一张图中,每一节点到另外一个节点都有一个权重(权重的意思就像从A节点到B节点需要花费一定的时间,而权重就是这个时间)这是一种用来求两点之间最小总权重路径的算法(当然也可以求最大)。
7.3步骤
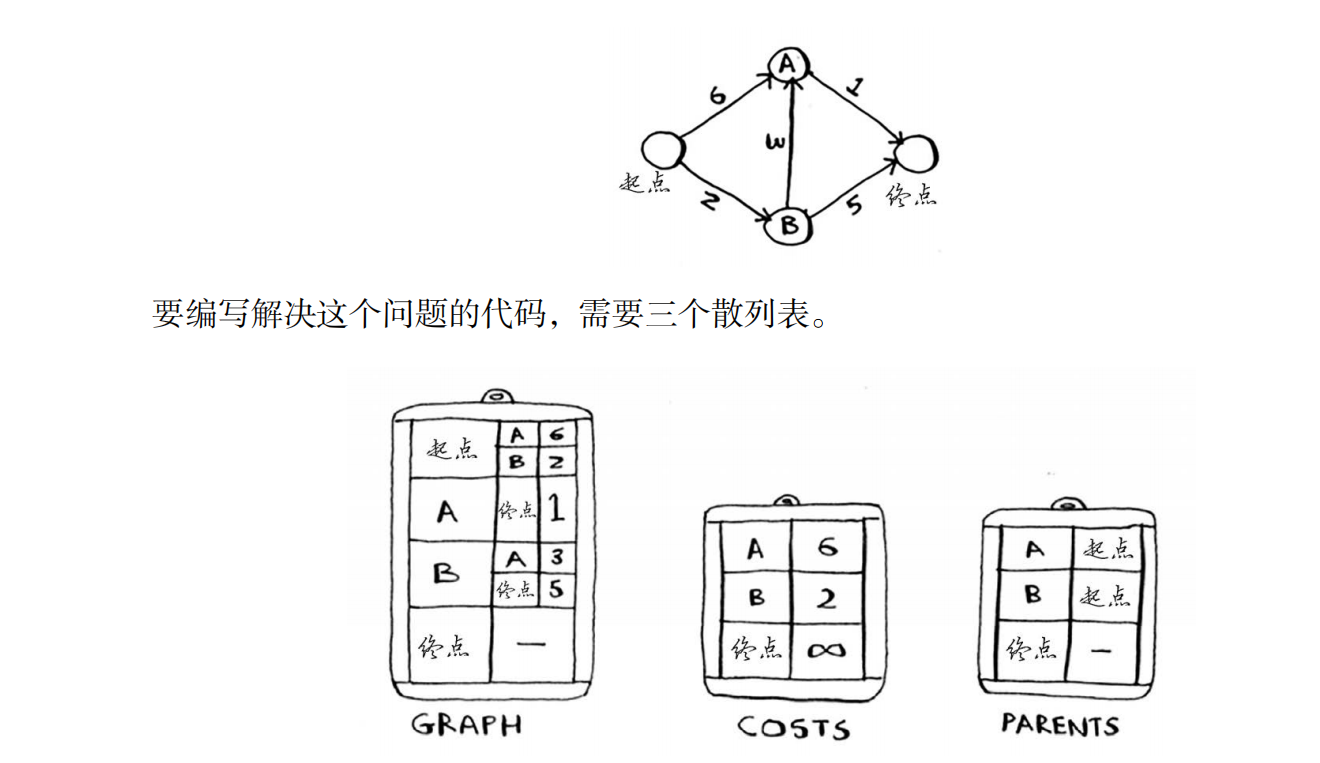
第一步
找出最小开销的节点(需要注意的是一开始并不是在图上的所有的点寻找,而是从起点《起点的开销为0》开始寻找,因为后面的子节点的开销你还不知道是多少,所以一开始我们还不知道开销是多少的子节点设为无穷大)
第二步
遍历最小开销节点所指向的所有子节点,并检测最小开销节点到该子节点上的开销是否小于原有的开销,如果小于就用当前开销替换原有开销,并且把该子节点的父节点指向该最小开销节点。(一开始只是最小开销节点指向子节点,子节点并没有指向最小开销节点,子节点指向最小开销节点是为了找到最小开销的同时也能知道他的路径)
第三步
把当前最小开销节点标记为已使用,再次回到第一步,直到所有的节点都被标记为已使用,那么那个时候终点的开销就是最小开销。
7.4实例
第八章 贪婪算法
贪婪算法很简单:每步都采取最优的做法。
像下面这个例子,每一次都选择播放州最多的那个上广播台。
虽然贪婪算法不能总是打到最优解,但是结果总会是近似最优解。
简单例子

# 要覆盖的州
states_needed = set(['mt', 'wa', 'or', 'id', 'nv', 'ut', 'ca', 'az'])
# 广播台清单
stations = dict()
stations['KONE'] = set(['id', 'nv', 'ut'])
stations['KTWO'] = set(['wa', 'id', 'mt'])
stations['KTHREE'] = set(['or', 'nv', 'ca'])
stations['KFOUR'] = set(['nv', 'ut'])
stations['KFIVE'] = set(['ca', 'az'])
# 最终使用的广播台
final_stations = set()
while states_needed: # 当还有需要的州未覆盖的时候循环
best_station = None # 覆盖了最多未覆盖的州的广播台
states_covered = set() # 已经覆盖了的州的集合
# 遍历所有广播台,找出最佳广播台并且将他的覆盖州加入已覆盖的州的集合
for station, states_for_station in stations.items():
# 计算需要覆盖的州和每个广播台覆盖的州的交集
covered = states_needed & states_for_station
# 如果交集的州数量比已经覆盖的州的数量多
if len(covered) > len(states_covered):
best_station = station # 最佳广播台更新为这个广播台
states_covered = covered # 已覆盖的州更新为交集
states_needed -= states_covered # 更新为覆盖的州
final_stations.add(best_station) # 更新最终结果
print(final_stations)
第九章 动态规划
动态规划先解决子问题,再逐步解决大问题。
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。后续可能会有评论区,不过也可以在github联系我。